3/26/12 Aim: How do we indentify solids?

   How do we identify solids?


 Solid geometry
- solid geometry is the geometry of a 3 dimentional space that has width , height and lenght
Examples:

Properties
-solids contain properties such as :
     - Volume ( how much water the container holds )
     - surface area ( the area you have to paint)
There are two main types of solids : Polyhedra & Non- Polyhedra
polyhedra - must have flat faces
Example : prisims, pyramids ect...

Non-polyhedra - has no flat faces of surfaces
Examples:  spheres, cones, cylinders ect...

Cross sections
- a cross sections is the shape that you get when you cut straight across a a figure or object







                                                Citations
Keppleri, Ioannis Constructability and Congruence , Harmonices MVNDI, http://wlym.com/~animations/harmonies/site.php?goto=congruence.html , 2006

Rock cycle minerals pre-lab, http://msnucleus.org/membership/html/k-6/rc/minerals/3/rcm3_1a.html

Mifflin, Houghton, Math Background, http://www.eduplace.com/math/mw/background/3/07/te_3_07_overview.html

3/19/12 Aim ; How do we find the are of a regular polygon

How do we find the are of a regular polygon?

Regular polygon conjecture
- The area of a regular polygon is given by the formula 1/2nas
- 'n' represent the number of sides , 'a' represents the apothem or could also be radius if applied to circles and 's' represents the side
- you can also use 1/2PA , 'P' represents the perimeter,'A' represents the area
Examples: 

Example question:

If  the apothem or 'a' = 6 , 's' = 12 and it has 8 sides ( octogon) what is the area?


















                                                              Citations
Wiley, John Sizing up the area of a polygon, Dummies.com , http://www.dummies.com/how-to/content/sizing-up-the-area-of-a-polygon.html

Regular polygons , Icoachmath.com , http://www.icoachmath.com/math_dictionary/Regular_Polygon.html

3/12/12 Aim : How do we calculate the area of triangles and rectangles?

How do we calculate the area of triangles and rectangles ?
   
                                                        Area 
- the are of a plane figure is the measure of the region endosed by the figure
- You can measure the area of a figure by counting the number of square units that arrange to completely fill the figure
Examples :

- For the area of a rectangle use the formula A= bh
- 'b' represents the base while 'h' represents the height of the rectangle

                 -For the area of a triangle use the formula A= 1/2bh or A= bh/2
        - 'b' represents the base while 'h' represents the height of the triangle







Example question :

 B= 12
 H= 8
 Area = ?





















                                                               Citations
Math salamanders, http://www.math-salamanders.com/shapes-clipart.html , 2010 -2011

Math planet , http://www.mathplanet.com/education/pre-algebra/introducing-geometry/triangles

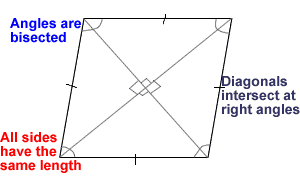
3/ Aim : How do we find the area of kites an trapezoids

How do we Find the Area of Kites and Trapezoids?

 Kites
- a kite has two pairs of equal sides that are both adjacent
- the formula to find the area of a kite goes by its diagonals  (d1+ d2 ) then you divide by 2

Example:

Example question:

 D1 = 6
D2 = 12
A= ?
















Trapezoids
- A trapezoid is a form of quadrilateril that has only one pair of parallel sides
- The formula you use to calculate the area is ( B1+ B2) divide by 2 then mutiply by the hieght of the trapezoid
Example:

Example question : 

Work citations 

Wilcox, Ted , Free Math Help , http://www.freemathhelp.com/feliz-special-parallelograms.html , 2011

Math warehouse, http://www.mathwarehouse.com/geometry/quadrilaterals/trapezoid.php

Bass, J.H, Drawing Geometrical Figures in Logo ,http://pages.intnet.mu/jhbpage/Program/Logo/tutorial/geometry.htm

Sparknotes, http://www.sparknotes.com/math/geometry2/measurements/section4.rhtml , 2012

3/15/12 Aim:How do we find the area of parallelograms?

How do we find the area of parallelograms?

 Parallelograms
- four sided shape with parallel opposite side
- to get the area of a parallelogram use the formula  A= bh
- 'b' represents the base of the parallelogram
- 'h' represents the height of the parallelogram

Example : The sides with the red arrows are the bases of the parallelograms and the the sides with the blue arrows are the hieght of the parallelogram

Example question:

 H= 6
B= 14
A= ?









Work citations 
http://www.ies.co.jp/math/products/geo1/applets/para/para.html

3/12/12 Aim: How do we Calculate the Area of Rectangles snd Triangles?

How do we Calculate the Area of Rectangles snd Triangles?

Area

- The are of a plane figure is the measure of the region endosed by the figure. 

- You can measure the area of a figure by counting the number of square units that are arranged to completely fill the figure

Triangles

- The area of a triangle is given by the formula : A= 1/2bh 

- ' b' in the formula represents the base of the triangles

- 'h' in the formula represents the hieght of the triangle

Example: In the example below the line 'BD' inside the triangle in represents the height of the triangle an line ' AC' represent the base

Example question :

A= 31.5

H= 7 

B= ?

Rectangles ( parallelograms)

- Have two pair of parallel sides

-  Use the formula A= bh to find the area

- ' B' represents the base

- 'H' represents the height

 Example:

Example Question : 

B= 10

H= 5

A= ?

Work citations

Math planet , http://www.mathplanet.com/education/geometry/right-triangles-and-trigonometry/mean-and-geometry , Spring 2011

Pierce, Rod. "About The Ads" Math Is Fun. Ed. Rod Pierce. 7 Aug 2011. 19 Mar 2012 <http://www.mathsisfun.com/about-ads.html>

aim#8 locus of points

How do we find the locus of points?

Locus of Points

- the locus of points is the set of all points that satisfy a condition

- it is a general graph of a given condition

- the locus of points equidistant from a single point is a set of points equidistant from the point in every direction ( A circle with the original point: its center  )

Example :

What is the locus of points from two fixed points ?

- The locus of pointa equidistant  from 2 fixed points is the perpendicular bisector of the line segment connecting those two points ( A line through the middle of two points)

Example: 

One line : What is the locus of points equidistant from a single line?

- the locus of points equidistant from a single line are two lines on opposite or either side , equidistant and parallel to that line

Example:

Two Parallel Lines : What is the locus of points equidistant from two parallel lines ?

-the locus of points equidistant from two parallel lines is another line, half way between both lines and is parallel

Example:

Two intersecting lines : What is the locus of points equidistant from 2 intersecting lines?

-the locus of points equidistant from 2 intersecting lines are two additional lines that bisect the angles formed by original lines ( two intersecting lines half way between the 2 original lines)

Example:

aim#7 logic2

How do we solve problems using logic?

-With logic there are 4 different forms that you can incorporate in sentences through different forms of conditionals

 Conditional
- the most frequently used statement in the construction of an arguement of the study of mathematics
- when you incorporate 'if' and ' then'
- when you write that if one thing happens, another has to follow
Ex:
Original statement : The sky is gray, it will rain.
Conditional: IF the sky is gray , THEN it will rain

Converse
- the converse is the opposite of a conditional
Ex: 
Conditional: If the sky is gray then it will rain
Converse:  If it rains then the sky is gray

Inverse
-using the inverse for of conditional , you are incorporating the word ' not' into the sentence
Ex:
Original statement: If it is raining , then you will need an umbrella
Inverse: If it is NOT raining , then you will NOT need an umbrella

Contrapositive
- this type of conditional is like the inverse when you incorporate the word 'not' but the statement is backwards
Ex: 
Original statement: If it is raining, then you will need an umbrella
Contrapositive: If you do not need and umbrella, then it is not raining

aim#6 logic1

What is a Mathematical statement?

Mathematical statment
- A mathematical statement is a statement that can be judged to be true or false
 Ex: The sky is green
   - since this statement has no truth value , it is a false mathematical statement
   -   The sky is blue 
   - Since this statement does have a truth value , it is a true mathematical statement
Negations
- they always have the opposite truth value of the original statement
- both statement need to be true to have truth value
Ex:
 Original statement : The sky is blue 
Negations: The sky is not blue

Conjunction
- a conjunction is when you take two sentences and put together using the word ' and'
Ex: 
Original statement: The sky is blue , the clouds are white
Conjunction: The sky is blue and the coulds are white