12/4/12 how do we rationalize a denominator?

How do we rationalize a denominator?

There are two different ways you can rationalize a denominator , first understand that you can never have a radical as a square root for example : 5 over radical 9

- in order to solve this you would have to simplify the bottom by finding the square root so this becomes 5/3

Then you might come to more complex problems like 5/3+(rad.)2
the way you would solve this problem is by using the complex conjugate of the denominator so you would have (3+(rad)2)(3-(rad)2) then FOIL this
the foiled product would be ; 9-3(rad)2+3(rad)2-(rad)4 , next you need to combine like terms and the final product 11
Now you need to multiple the same number on the bottom to the top so it would be (5)(3-(rad.)2)
 this results to 15-5(rad)2/11 as the final product

11/28/12 how do we factor by grouping ?

How do we factor by grouping ?

- When you factor your taking out common terms so you need to group them , for example :
x^3+3x^2-4x-12
First factor the first half of the equation : x^3+3x^2
this becomes : x^2(x+3) because you take out the common factor and make it so that if you foil it you get what the original half of the equation was.
Second ,now you do the same thing to the other half of the equation: 4x-12
this becomes 4(x+3) because four can come out of each term
Third , you can now combine like terms (x^2 +4) (x+3)
but one of the terms can be simplified still so;
 The final equation becomes (x+2)(x+2)(x+3)

absolute value inequalities 9/13/12

How do we solve absolute value inequalities ?

-The purpose of absolute value is to change negative numbers to postive numbers
-When applying absolute value to inequalites you will have 2 'x' values representing the absolute value Example:
solve for 'x"1st:  l 5x-7 l>8
add 7 to both sides : l 5x l >15
then divide 5 from both sides to isolate the x :
l x l>3
Now you need to flip the signs:
 l 5x-7 l<-8
add 7 to both sides:
l 5x l <-1
now divide 5 from both sides to isolate 'x'
l x l <-1
Your results are :
l x l <-1
l x l <-8

imaginary numbers

How do we use imaginary numbers ?

-We define the square root of -1 as "i". This is also called an imaginary unit.
-We call the 'i' solution to the equation ; i^2+1=0

Simplfying imaginary numbers example
What is the square root of -25 ?
- first notice that there shouldnt be any negative numbers under a radical , this means that there is no real solution , so your going to solve for the no solution.
 so this will simplify to |25 and |-1
Now that 'i' is equivalent to the square root of -1 you can plug it in so the result will be 5i

What is the square root of -17?
this simplifies to |17 & |-1
now use 'i' in place of negative -1 and this becomes ; i|17

Notice that when the number is rational 'i' goes after the number and when the number is irrational the'i' goes before the number.




Note : there was no radical sign so I used "|" in place of it

The discriminant (10/23/12)

How do we apply our quadratic knowledge to real world situations? 

The quadratic equation :

Underneath the radical of the quadratic equation above, lies The Discriminant 
B^2- 4ac
Rules of the discriminant :
b^2-4ac>0 - you'll get 2 solutions
b^2-4ac=0 - you'll get 1 solution
b^2-4ac<0 - you get 0 solutions

For example:  x ^2 + 6x +9=0
label the letters to solve using the discriminant:
a=1
b=6
c=9
now plug it into the equation:
6^2-4(1)(-9) = 72
- referring back to the rules of the discriminant , the solution is greater than 0 so it has two solutions

-If b^2-4ac is a perfect square the two roots will be rational when you graph them
For example: x^2 +6x+8
a=1
b=6
c=8
plug into the formula : 6^2-4(1)(8)
the result is 4, since its a perfect square its rational

Next example: x^2 +3x-1
a=1
b=3
c=-1
plug into the formula :3^2-4(1)(-1)
this becomes: 9-4(1)(-1)
the result is 13 , since its not a perfect square its irrational


















Cited works :
Let's be clear,http://paulpietrzak.blogspot.com/2011/01/solving-quadratic-equations-quadratic.html

inverse of functions (10/3/12)

How do we calculate the inverse of functions?

- Two operations are said to be the inverse of each other if one of the operations undoes the other 

-The inverse of f(x) can be calculated by swtiching the x & y values
For example : What is the inverse if f(x)=2x?
 y=2x -------> x=2y
Then solve :
x/2=2y/2 ( the 2's on the right cancel out)
this then equals : x/2=y

- Using the inverse can also be applied to coordinates by switching the x & y as well
 For example : What is the inverse of { (3,2)(-2,5)(6,0)}?
This equals : {(2,3)(5,-2)(0,6)}

Quadratic equation

10/19/12
Aim: How do we solve quadratic equations?

Every parabola has an Axis of symmetry and a Vertex for example :

In order to determine the axis of symmetry , when given an equation you need to solve for (x).
- to solve for (x); use the equation (-b/2a)
Try this :
y=x^2 +6x+8
First label each of the variables to make it more clear :
a=1
b=6
c=8
Now you can use these numbers to solve for the axis of symmetry:
-6/2(1) ----> -6/3 = -2
The axis of symmetry/(x) = -2

Now using the (x) value you can solve for the vertex by plugging it into the equation
y=(-2)^2 + 6(-2)+8
y=0
This gives you the coordinate of the vertex : (-2,0)

















Workcite 
Northstarmath, http://www.northstarmath.com/sitemap/parabola.html

5/3/12 How do we find the area of sectors and other parts of a circle?

How do we find the area of sectors and other parts of a circle?

Sector of a circle
- a sector of a circle is the region between the radii and the arc of a sector
To find the area of a sector : # of degrees /360 x (pi) r^2
Ex:

Segment of a circle 
- a segment of a circle is the region between a chord and arc of circle
To find the area of the segment of a circle : # of degrees/360 x  (pi)r^ - 1/2bh
Ex:

Annulus 
- an annulus is the region between two concentric circles
To find the area of the annulus : (pi)R^2- (pi)r1

Ex:

Practice question : If radius 1 is 12 and radius 2 is 6, What is the area of the annulus?

                                                           Citations
- Problem solving , http://www.p12.nysed.gov/ciai/mst/math/sampletasks/Math6Sample.htm
- Chord and segment of a circle, http://www.winpossible.com/lessons/Chord_and_Segment_Of_A_Circle.aspx, 2011
- Annulus calculator , http://www.calculatorsoup.com/calculators/geometry-plane/annulus.php

5/1/12 How do we use secant , chord and tangents in circles? ?

How do we use Secants, Chords and Tangents in circles?

Secant
- a line that cuts through or divides a curve into two or more parts
Ex:

Chord
- a straight line thats joins the ends of an arc
Ex :

Tangent
-  straight line or plane that touches a curve or curved surface at a point
Ex:

Practice Question : What does the line TL image below represent?

                                                                       Citations 
- Chord , Wolfram MathWorld , http://mathworld.wolfram.com/Chord.html , 2012

- http://www.google.com/imgres?q=secant&start=173&um=1&hl=en&sa=N&biw=1280&bih=861&addh=36&tbm=isch&tbnid=Lo2YH7az3PTd1M:&imgrefurl=https://internal.shenton.wa.edu.au/maths/WestOne3CMAS/content/004_functions/media/glossary.html&docid=r1W_zcdlQ_KVDM&imgurl=https://internal.shenton.wa.edu.au/maths/WestOne3CMAS/content/004_functions/media/images/glossary_secant.gif&w=290&h=250&ei=QcymT8myJqGJ6QGyiaCdBA&zoom=1&iact=hc&vpx=606&vpy=126&dur=282&hovh=179&hovw=216&tx=126&ty=147&sig=100793830460579110965&page=8&tbnh=152&tbnw=195&ndsp=25&ved=1t:429,r:7,s:173,i:194

- Chapter 9: Chords and Arcs, http://whites-geometry-wiki.wikispaces.com/PETO626
- Geometry : Circles , http://www.sparknotes.com/math/geometry1/circles/section3.rhtml , 2012

How do we review transformations?

Isometry

- length is preserved

- sides are congruents ( like their reflecting)

Ex:                         

              

Direct isometry 

- orientation is preserved( stays the same)

-  The order of the lettering in the figure and the images are the same 

- either clockwise becomes counter clockwise or counter clockwise becomes clockwise 

- every translation and rotation is a direct isometry

Ex: 

Opposite isometry

- orientation isn't preserved (changes)

-  the order of the lettering is reversed

- every reflection and glide reflection is an opposite isometry 

 Ex:

Same orientation :

 rorgin (x,y) -> (-x,-y)              

 R90 (x,y) -> (-y,x)

 R180 ( x,y)-> (-x,-y)

 R270 ( x,y) -> ( y,-x)

Reversed orientation:

 r- x-axis (x,y) -> ( x,-y)

 r-y-axis (x,y) ->(-x,y)

ry = x (x,y) -> ( y,x)

ry = -x (x,y) -> (-y,-x)

Practice question : What is the difference between a direct and opposite isometry?

                                                      Citations 

- http://zsolania.blogspot.com/

- Haskell , Kenn, Functional Lens , http://www.kennknowles.com/blog/2007/12/03/calculating-the-reflect-rotate-translate-normal-form-for-an-isometry-of-the-plane-in-haskell-and-verifying-it-with-quickcheck/

4/24/12 What are altitudes , perpendicular bisectors and angle bisectors?

What are Altitudes, Perpendicular bisectors and Angle bisectors?

                     


                                       Angle bisectors


- an angle bisector,bisects an angle in half creating two congruent angles
Ex:

                            Perpendicular Bisectors
- a line that cuts through another line going in the opposite direction or bisects a side
Ex:

                                           Altitudes 
- a line segment through a vertex that is perpendicular to a line containing side
- makes a right angle
- is the height of the triangle

Ex:

Practice question : If the given height of the triangle is 14, What is the length of the altitude ? Explain your answer.











                                                        Citations


       -Triangle angle  bisector theorem, Math warehouse ,http://www.mathwarehouse.com/geometry/similar/triangles/angle-bisector-theorem.php

- Perpendicular bisector - interactive applet , http://www.analyzemath.com/Geometry/PerpendicularBisector/PerpendicularBisector.html , April ,3 2011

- Triangles , bisectors and circumcircles - interactive applet , http://www.analyzemath.com/Geometry/Circumcircle/Circumcircle.html , April ,3 2011

- Miller , Maria , Altitude of a triangle , homeschoolmath.net , http://www.homeschoolmath.net/teaching/g/altitude.php , 2003-2012

4/18/12 How do you find the surface area and volume of a sphere?

How do you find the surface area and volume of a sphere?

                                            Spheres 
- a sphere is a set of all points in space equidistant from a point called the center
Ex :

- In order to calculate the surface area of a sphere use the formula : SA= 4(pi)r^2
      - 'r' represents the radius of the sphere
In order to calculate the volume of a sphere use the formula : 4(pi)r^2/3
      -'r' represents the radius

Practice question: If the given radius of a sphere is 4 , What is the surface area of the sphere?

                                               Citations
Unit math example: ( Geometric solids) , http://www.unitmath.com/um/p/Examples/GeometricSolids/GeometricSolids.html ,  9/10/2000

3/29/12 How do we find the the surface area and lateral area of pyramids and cones?

How do we find the surface area and lateral area of pyramids and cones?

 Pyramids
- a pyramid is a solid that connects a polygon base to a point
- the slant height of a pyramid is the height of the lateral faces
Ex :

- you can calulate the lateral area of a pyramid by using the formula LA= 1/2pl
-'p' represents the perimeter
-'l' represents the slant height
- You can calculate the surface area


Cones
- the base of a cone is circle and the other end ( vertex) is pointed similar to a pyramid
- the slant height of a cone is the distance from the vertex to a point on the base
Ex:

- to calculate the lateral area of a cone use the formula (pi)rl
- 'r' represents the radius
-'l' represents the slant height
- In order to calculate the surface area , and extra steps need to be included
- use the formula SA= LA(lateral area) + B (base)
- to find the base use (pi)r^2 , then plug in the final number in the formula above this one

Practice Question: If the radius of a cone 'r' is 4 and the slant height 'l' is 12 , What is the the lateral area of a cone?










                                                         Citations
- Geometry help!!! triangular pyramid , MHF,http://mathhelpforum.com/geometry/27562-solved-geometry-help-triangular-pyramid.html , 2005-2012

- Ring my bell- Volume of cone , Lesson poly , Silicon valley education foundation, http://www.lessonopoly.org/node/2299 , 2010

3/27/12 How do we find surface area and lateral area of prisms and cylinders?

How do we find surface area and lateral area of prisms and cylinders?

 Prisms
- a prism is a solid figure with bases that are 2 congruent polygons
- the other sides of the prism are called  lateral faces
- a prism  is named by the shape of its bases
Ex:

- calculate the surface area of a prism by using the formula SA= LA+ 2B
 - " LA" represents the lateral area
- " B' represents the base
- Calculate the lateral are of a prism by using LA = ph
 - 'P' represents perimeter of a base
 - 'H' represents the height

Cylinders
Ex:

- calculate the lateral area using the formula 2(pi)rh
-'r' represents the radius
-' h' represents the height

- In order to calculate the the surface area multiple steps are made
- calculate the area of the base by using (pi)r^2
         - 'r' represents the radius
- multiple your answer by 2
- you then take your lateral area and add that with the number of the bases
    - you can go by this formula to calculate the sureface area of a cylinder  SA= LA +2B
-'LA' represents the lateral area
-'B' represents the base

Practice question : If the radius 'r' of a cylinder is 6 and the height ' h' is 4 , what is the lateral area of a cylinder?



                                           




                                            Citations 
-The 48 special crystal forms , University of wisconsin , greenbay , 1/20/11 , http://www.uwgb.edu/dutchs/symmetry/xlforms.htm

- Volume of a cylinder , Math homework series on geometry help , http://www.geometry-help.info/Volume_of_a_Cylinder.html, 2009

3/26/12 Aim: How do we indentify solids?

   How do we identify solids?


 Solid geometry
- solid geometry is the geometry of a 3 dimentional space that has width , height and lenght
Examples:

Properties
-solids contain properties such as :
     - Volume ( how much water the container holds )
     - surface area ( the area you have to paint)
There are two main types of solids : Polyhedra & Non- Polyhedra
polyhedra - must have flat faces
Example : prisims, pyramids ect...

Non-polyhedra - has no flat faces of surfaces
Examples:  spheres, cones, cylinders ect...

Cross sections
- a cross sections is the shape that you get when you cut straight across a a figure or object







                                                Citations
Keppleri, Ioannis Constructability and Congruence , Harmonices MVNDI, http://wlym.com/~animations/harmonies/site.php?goto=congruence.html , 2006

Rock cycle minerals pre-lab, http://msnucleus.org/membership/html/k-6/rc/minerals/3/rcm3_1a.html

Mifflin, Houghton, Math Background, http://www.eduplace.com/math/mw/background/3/07/te_3_07_overview.html

3/19/12 Aim ; How do we find the are of a regular polygon

How do we find the are of a regular polygon?

Regular polygon conjecture
- The area of a regular polygon is given by the formula 1/2nas
- 'n' represent the number of sides , 'a' represents the apothem or could also be radius if applied to circles and 's' represents the side
- you can also use 1/2PA , 'P' represents the perimeter,'A' represents the area
Examples: 

Example question:

If  the apothem or 'a' = 6 , 's' = 12 and it has 8 sides ( octogon) what is the area?


















                                                              Citations
Wiley, John Sizing up the area of a polygon, Dummies.com , http://www.dummies.com/how-to/content/sizing-up-the-area-of-a-polygon.html

Regular polygons , Icoachmath.com , http://www.icoachmath.com/math_dictionary/Regular_Polygon.html

3/12/12 Aim : How do we calculate the area of triangles and rectangles?

How do we calculate the area of triangles and rectangles ?
   
                                                        Area 
- the are of a plane figure is the measure of the region endosed by the figure
- You can measure the area of a figure by counting the number of square units that arrange to completely fill the figure
Examples :

- For the area of a rectangle use the formula A= bh
- 'b' represents the base while 'h' represents the height of the rectangle

                 -For the area of a triangle use the formula A= 1/2bh or A= bh/2
        - 'b' represents the base while 'h' represents the height of the triangle







Example question :

 B= 12
 H= 8
 Area = ?





















                                                               Citations
Math salamanders, http://www.math-salamanders.com/shapes-clipart.html , 2010 -2011

Math planet , http://www.mathplanet.com/education/pre-algebra/introducing-geometry/triangles

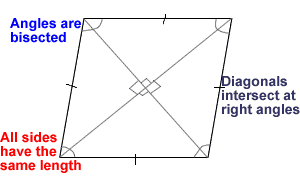
3/ Aim : How do we find the area of kites an trapezoids

How do we Find the Area of Kites and Trapezoids?

 Kites
- a kite has two pairs of equal sides that are both adjacent
- the formula to find the area of a kite goes by its diagonals  (d1+ d2 ) then you divide by 2

Example:

Example question:

 D1 = 6
D2 = 12
A= ?
















Trapezoids
- A trapezoid is a form of quadrilateril that has only one pair of parallel sides
- The formula you use to calculate the area is ( B1+ B2) divide by 2 then mutiply by the hieght of the trapezoid
Example:

Example question : 

Work citations 

Wilcox, Ted , Free Math Help , http://www.freemathhelp.com/feliz-special-parallelograms.html , 2011

Math warehouse, http://www.mathwarehouse.com/geometry/quadrilaterals/trapezoid.php

Bass, J.H, Drawing Geometrical Figures in Logo ,http://pages.intnet.mu/jhbpage/Program/Logo/tutorial/geometry.htm

Sparknotes, http://www.sparknotes.com/math/geometry2/measurements/section4.rhtml , 2012

3/15/12 Aim:How do we find the area of parallelograms?

How do we find the area of parallelograms?

 Parallelograms
- four sided shape with parallel opposite side
- to get the area of a parallelogram use the formula  A= bh
- 'b' represents the base of the parallelogram
- 'h' represents the height of the parallelogram

Example : The sides with the red arrows are the bases of the parallelograms and the the sides with the blue arrows are the hieght of the parallelogram

Example question:

 H= 6
B= 14
A= ?









Work citations 
http://www.ies.co.jp/math/products/geo1/applets/para/para.html

3/12/12 Aim: How do we Calculate the Area of Rectangles snd Triangles?

How do we Calculate the Area of Rectangles snd Triangles?

Area

- The are of a plane figure is the measure of the region endosed by the figure. 

- You can measure the area of a figure by counting the number of square units that are arranged to completely fill the figure

Triangles

- The area of a triangle is given by the formula : A= 1/2bh 

- ' b' in the formula represents the base of the triangles

- 'h' in the formula represents the hieght of the triangle

Example: In the example below the line 'BD' inside the triangle in represents the height of the triangle an line ' AC' represent the base

Example question :

A= 31.5

H= 7 

B= ?

Rectangles ( parallelograms)

- Have two pair of parallel sides

-  Use the formula A= bh to find the area

- ' B' represents the base

- 'H' represents the height

 Example:

Example Question : 

B= 10

H= 5

A= ?

Work citations

Math planet , http://www.mathplanet.com/education/geometry/right-triangles-and-trigonometry/mean-and-geometry , Spring 2011

Pierce, Rod. "About The Ads" Math Is Fun. Ed. Rod Pierce. 7 Aug 2011. 19 Mar 2012 <http://www.mathsisfun.com/about-ads.html>

aim#8 locus of points

How do we find the locus of points?

Locus of Points

- the locus of points is the set of all points that satisfy a condition

- it is a general graph of a given condition

- the locus of points equidistant from a single point is a set of points equidistant from the point in every direction ( A circle with the original point: its center  )

Example :

What is the locus of points from two fixed points ?

- The locus of pointa equidistant  from 2 fixed points is the perpendicular bisector of the line segment connecting those two points ( A line through the middle of two points)

Example: 

One line : What is the locus of points equidistant from a single line?

- the locus of points equidistant from a single line are two lines on opposite or either side , equidistant and parallel to that line

Example:

Two Parallel Lines : What is the locus of points equidistant from two parallel lines ?

-the locus of points equidistant from two parallel lines is another line, half way between both lines and is parallel

Example:

Two intersecting lines : What is the locus of points equidistant from 2 intersecting lines?

-the locus of points equidistant from 2 intersecting lines are two additional lines that bisect the angles formed by original lines ( two intersecting lines half way between the 2 original lines)

Example:

aim#7 logic2

How do we solve problems using logic?

-With logic there are 4 different forms that you can incorporate in sentences through different forms of conditionals

 Conditional
- the most frequently used statement in the construction of an arguement of the study of mathematics
- when you incorporate 'if' and ' then'
- when you write that if one thing happens, another has to follow
Ex:
Original statement : The sky is gray, it will rain.
Conditional: IF the sky is gray , THEN it will rain

Converse
- the converse is the opposite of a conditional
Ex: 
Conditional: If the sky is gray then it will rain
Converse:  If it rains then the sky is gray

Inverse
-using the inverse for of conditional , you are incorporating the word ' not' into the sentence
Ex:
Original statement: If it is raining , then you will need an umbrella
Inverse: If it is NOT raining , then you will NOT need an umbrella

Contrapositive
- this type of conditional is like the inverse when you incorporate the word 'not' but the statement is backwards
Ex: 
Original statement: If it is raining, then you will need an umbrella
Contrapositive: If you do not need and umbrella, then it is not raining

aim#6 logic1

What is a Mathematical statement?

Mathematical statment
- A mathematical statement is a statement that can be judged to be true or false
 Ex: The sky is green
   - since this statement has no truth value , it is a false mathematical statement
   -   The sky is blue 
   - Since this statement does have a truth value , it is a true mathematical statement
Negations
- they always have the opposite truth value of the original statement
- both statement need to be true to have truth value
Ex:
 Original statement : The sky is blue 
Negations: The sky is not blue

Conjunction
- a conjunction is when you take two sentences and put together using the word ' and'
Ex: 
Original statement: The sky is blue , the clouds are white
Conjunction: The sky is blue and the coulds are white

Aim#5 glide reflection & Isometry

How do we use other definitions of transformations?


 Glide Reflection
- the combination of a reflection in a line and a translation along that line
Examples:

Isometry
- a transformation of the plane that preserves length
 -  a direct Isometry preserves orientations or order the letters on the diagram go in the same clockwise or counter clockwise direction on the figure and it's image .
Example :

 Opposite Isometry 
-changes the order such as the direction
Examples :